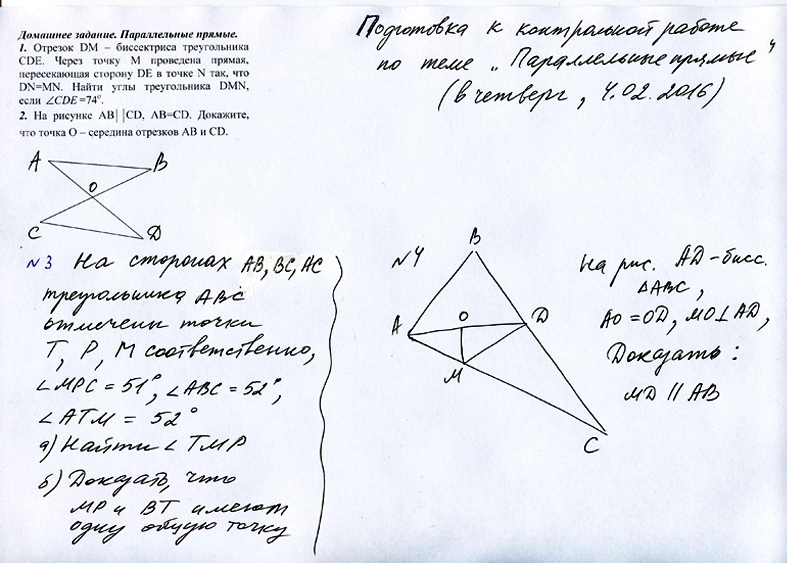
Домашнее задание по геометрии от Лизуновой В.А., подготовка к самостоятельной работе (02.02.2016)

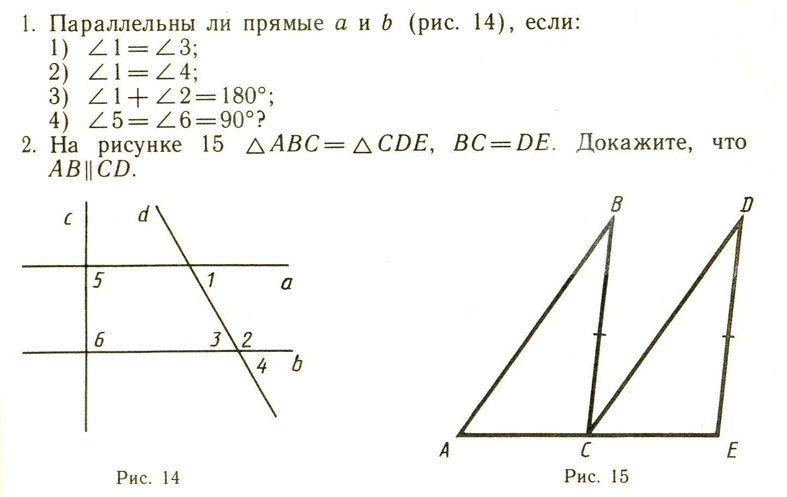
Домашнее задание по геометрии от Лизуновой В.А., подготовка к самостоятельной работе (29.01.2016)

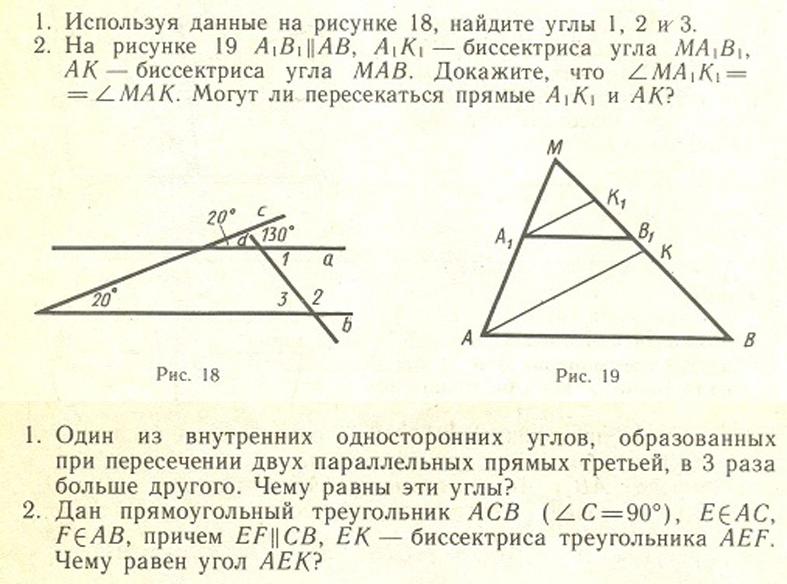
Домашнее задание по алгебре от Лизуновой В.А. (28.01.2016)

Для всех: №694,697,698,699,700,702,703, 777,778,781,782, готовимся к самостоятельной работе

Для кружка:

Первый тур ( 15 минут; каждая задача – 6 баллов)

1.1. Грузовик едет со скоростью 65 км/ч, а за ним едет легковой автомобиль - со скоростью 80 км/ч. На каком расстоянии друг от друга эти автомобили будут через две минуты после того, как легковой автомобиль догонит грузовик?.

1.2 Ваня задумал простое трехзначное число, все цифры которого различны. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух.

1.3. Из Москвы в Неаполь самолет вылетает в 9.20 по московскому времени, а прилетает в 11.30 по неаполитанскому. Из Неаполя в Москву самолет вылетает в 8.30 по неаполитанскому времени, а прилетает в 14.40 по московскому. Какова разница во времени между Москвой и Неаполем?

Второй тур ( 20 минут, каждая задача стоит 7 баллов)

2.1 Число умножили на сумму его цифр и получили2008. Найдите это число.

2.2. Точка В лежит на отрезке АС, причем AB = 2 см, BC = 1 см. На прямой АВ укажите все такие точки М, для которых AM + BM = CM.

2.3. Женя и Антон учатся в одном классе. У Антона одноклассников вчетверо больше, чем одноклассниц. А у Жени одноклассниц на 17 меньше, чем одноклассников. Кто Женя: девочка или мальчик?

Третий тур (25 минут, каждая задача стоит 8 баллов)

3.1. На прямой отметили несколько точек. После этого между каждыми двумя соседними точками поставили еще по точке. Аналогичную операцию проделали еще три раза. В результате, на прямой оказалось ровно 65 точек. Сколько точек было на прямой первоначально?

3.2 Разрежьте нарисованный пятиугольник на две одинаковые (совпадающие при наложении)части.

3.3. В вершинах треугольника записаны числа 1, 2 и 3. Затем каждое из чисел одновременно заменили на сумму двух соседних. Эту операцию проделали еще некоторое количество раз. Могла ли сумма получившихся в итоге трех чисел оказаться равной 3000000?